در قرن نوزدهم دو ریاضیدان بزرگ به نام «لباچفسکى» و «ریمان» دو نظام هندسى را صورت بندى کردند که هندسه را از سیطره اقلیدس خارج مى کرد. صورت بندى «اقلیدس» از هندسه تا قرن نوزدهم پررونق ترین کالاى فکرى بود و پنداشته مى شد که نظام اقلیدس یگانه نظامى است که امکان پذیر است. این نظام بى چون و چرا توصیفى درست از جهان انگاشته مى شد. هندسه اقلیدسى مدلى براى ساختار نظریه هاى علمى بود و نیوتن و دیگر دانشمندان از آن پیروى مى کردند. هندسه اقلیدسى بر پنج اصل موضوعه استوار است و قضایاى هندسه با توجه به این پنج اصل اثبات مى شوند. اصل موضوعه پنجم اقلیدس مى گوید: «به ازاى هر خط و نقطه اى خارج آن خط، یک خط و تنها یک خط به موازات آن خط مفروض مى تواند از آن نقطه عبور کند.» هندسه «لباچفسکى» و هندسه «ریمانى» این اصل موضوعه پنجم را مورد تردید قرار دادند. در هندسه «ریمانى» ممکن است خط صافى که موازى خط مفروض باشد از نقطه مورد نظر عبور نکند و در هندسه «لباچفسکى» ممکن است بیش از یک خط از آن نقطه عبور کند. با اندکى تسامح مى توان گفت این دو هندسه منحنى وار هستند. بدین معنا که کوتاه ترین فاصله بین دو نقطه یک منحنى است.
هندسه اقلیدسى فضایى را مفروض مى گیرد که هیچ گونه خمیدگى و انحنا ندارد. اما نظام هندسى لباچفسکى و ریمانى این خمیدگى را مفروض مى گیرند. (مانند سطح یک کره) همچنین در هندسه هاى نااقلیدسى جمع زوایاى مثلث برابر با ۱۸۰ درجه نیست. (در هندسه اقلیدسى جمع زوایاى مثلث برابر با ۱۸۰ درجه است.) ظهور این هندسه هاى عجیب و غریب براى ریاضیدانان جالب توجه بود اما اهمیت آنها وقتى روشن شد که نسبیت عام اینشتین توسط بیشتر فیزیکدانان به عنوان جایگزینى براى نظریه نیوتن از مکان، زمان و گرانش پذیرفته شد. چون صورت بندى نسبیت عام اینشتین مبتنى بر هندسه «ریمانى» است. در این نظریه هندسه زمان و مکان به جاى آن که صاف باشد منحنى است. نظریه نسبیت خاص اینشتین تمایز آشکارى میان ریاضیات محض و ریاضیات کاربردى است. هندسه محض مطالعه سیستم هاى ریاضى مختلف است که به وسیله نظام هاى اصول موضوعه متفاوتى توصیف شده اند. برخى از آنها چندبعدى و یا حتى nبعدى هستند. اما هندسه محض انتزاعى است و هیچ ربطى با جهان مادى ندارد یعنى فقط به روابط مفاهیم ریاضى با همدیگر، بدون ارجاع به تجربه مى پردازد. هندسه کاربردى، کاربرد ریاضیات در واقعیت است. هندسه کاربردى به وسیله تجربه فراگرفته مى شود و مفاهیم انتزاعى برحسب عناصرى تفسیر مى شوند که بازتاب جهان تجربه اند. نظریه نسبیت، تفسیرى منسجم از مفهوم حرکت، زمان و مکان به ما مى دهد. اینشتین براى تبیین حرکت نور از هندسه نااقلیدسى استفاده کرد. بدین منظور هندسه «ریمانى» را برگزید.
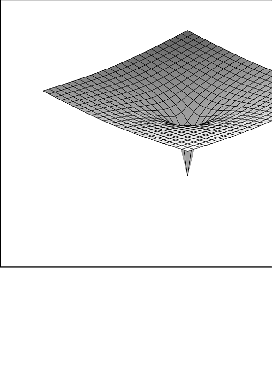
هندسه اقلیدسى براى دستگاهى مشتمل بر خط هاى راست در یک صفحه طرح ریزى شده است اما در عالم واقع یک چنین خط هاى راستى وجود ندارد. اینشتین معتقد بود امور واقع هندسه ریمانى را اقتضا کرده اند. نور بر اثر میدان هاى گرانشى خمیده شده و به صورت منحنى در مى آید یعنى سیر نور مستقیم نیست بلکه به صورت منحنى ها و دایره هاى عظیمى است که سطح کرات آنها را پدید آورده اند. نور به سبب میدان هاى گرانشى که بر اثر اجرام آسمانى پدید مى آید خط سیرى منحنى دارد. براساس نسبیت عام نور در راستاى کوتاه ترین خطوط بین نقاط حرکت مى کند اما گاهى این خطوط منحنى هستند چون حضور ماده موجب انحنا در مکان - زمان مى شود.
در نظریه نسبیت عام گرانش یک نیرو نیست بلکه نامى است که ما به اثر انحناى زمان _ مکان بر حرکت اشیا اطلاق مى کنیم. آزمون هاى عملى ثابت کردند که شالوده عالم نااقلیدسى است و شاید نظریه نسبیت عام بهترین راهنمایى باشد که ما با آن مى توانیم اشیا را مشاهده کنیم. اما مدافعین هندسه اقلیدسى معتقد بودند که به وسیله آزمایش نمى توان تصمیم گرفت که ساختار هندسى جهان اقلیدسى است یا نااقلیدسى. چون مى توان نیروهایى به سیستم مبتنى بر هندسه اقلیدسى اضافه کرد به طورى که شبیه اثرات ساختار نااقلیدسى باشد. نیروهایى که اندازه گیرى هاى ما از طول و زمان را چنان تغییر دهند که پدیده هایى سازگار با زمان - مکان خمیده به وجود آید. این نظریه به «قراردادگرایى» مشهور است که نخستین بار از طرف ریاضیدان و فیزیکدان فرانسوى «هنرى پوانکاره» ابراز شد. اما نظریه هایى که بدین طریق به دست مى آوریم ممکن است کاملاً جعلى و موقتى باشند. اما دلایل کافى براى رد آنها وجود دارد؟

نوشته شده توسط رافق مجتهدزاده خیاوی در دوشنبه 86/8/14 و ساعت 1:10 عصر |
نظرات دیگران()




