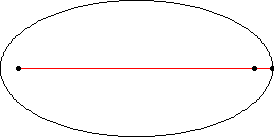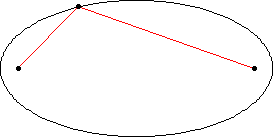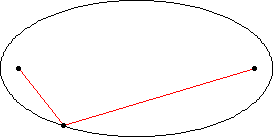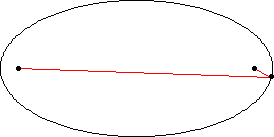
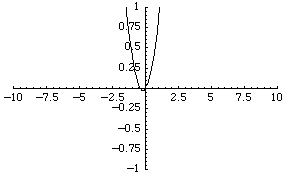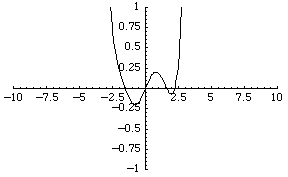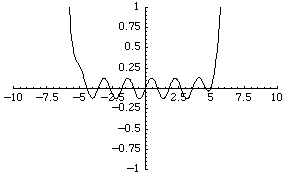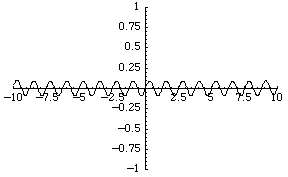قطار های مدل اغلب داری دو نوع ریل هستند : ریل های خمیده ، که در بیشتر اوقات کمان هایی از یک دایره به شعاع R هستند ، و ریل های راست. این ریل ها عمدتا طوری طراحی شده اند که به شکل زیر سرهم بندی می شود
مسیر های AB و CDمستقیم و مسیرهای BC و DAنیم دایره هستند.اما آیا این مسیر ها به اندازه کافی خمیده هستند ؟!
مسیر های طراحی شده بوسیله اصطکاک پایدار می ماند و اغلب ممکن است در هنگام عبور قطار از روی آنها جدا شوند.اگر چه ممکن است در وسط مسیر های خمیده یا مسیر های مستقیم اتصالات دیگری نیز وجود داشته باشد ولی در بیشتر مواقع مسیر کلی از نقاط A,B,C,D جدا می شود .
برای بررسی این اتفاق تصور کنید قطاری با سرعت ثابت در حال حرکت است بنابراین شتاب مماس آن یعنی صفر است و در نتیجه شتاب کلی آن تنها شتاب مرکز گرای آن است( شعاع خمیدگی مسیر است که برای شکل بالا بر روی مسیر خمیده مقداری برابر R دارد).بنابراین اندازه شتاب بر روی مسیر مستقیم صفر است و در مسیر نیم دایره است.به این دلیل مقدار شتاب در نقاط A,B,C,D نا پیوسته است (همانطور که در نمودار مشخص است). همین نا پیوستگی سبب می شود تا نیروی عکس العملی که از جانب قطار به ریل وارد می شود نیز در این نقاط نا پیوسته باشد . به همین دلیل نوعی شوک یا ضربه به هنگام وارد شدن و یا ترک پیچ وجود دارد ( البته حتما اثر این ضربه را در پیچ های غیر اصولی هنگام عبور خودرو و یا برعکس نیروی نرم و یکنواختی را در هنگام سفر در داخل مترو حس کرده اید) برای جلوگیری از بوجود آمدن چنین نقاط فشاری که موجب خروج قطار از ریل و یا خروج خودرو از جاده می شود مسیرها می بایست طوری طراحی شوند که خمیدگی جاده بطور یکنواخت تغییر کند.( البته این طراحی بطور نسبی و با توجه به شرایط محیطی و کمک گرفتن از شیب و اتصالات قوی تر نیز قابل بهبود است )
مثال : مسیری در امتداد منفی محور x ها و مسیر دیگری در امتداد شعاع y=x-1 ، x?2 وجود دارد می خواهیم این دو مسیر را با استفاده از منحنی چند جمله ای f، به اندازه کافی خمیده و با حد اقل درجه ، طوری بهم وصل کنیم که هیچ گونه نا پیوستگی شتاب در نقاط اتصال احساس نشود.
راه حل : منحنی f باید طور انتخاب شود که مسیر ، شیب و خمیدگی آن در نقاط x=0 و x=2 پیوسته باشد.(همانطور که می دانیم خمیدگی عکس شعاع خم است )از آنجا که خمیدگی ( curvature ) منحنی f بصورت زیر است
و f چند جمله است ما تنها نیاز داریم f و "f و ""f در نقاط اتصال به y=0 ، x?0 و y=x-1 ، x?2 مقادیر y و "y و ""y را داشته باشد تا پیوستگی های مورد نظر اعمال شود یعنی هم مسیر پیوسته شود و هم از پیوستگی f" و f"" پیوستگی نتیجه شود و بنابراین و شتاب کل پیوسته می شود.
y(0)=f(0)=0 y"(0)=f"(0)=0 y""(0)=f""(0)=0
y(2)=f(2)=1 y"(2)=f"(2)=1 y""(2)=f""(2)=0
این شش شرط مستقل به ما چند جمله ای درجه 5 را پیشنهاد می کند :
f(x)=A+Bx+Cx2+Dx3+Ex4+Fx5
f"(x)=B+2Cx+3Dx2+4Ex3+5Fx4
f""(x)=2C+6Dx+12Ex2+20Fx3
سه شرط x=0 ، A=B=C=0 را نتیجه میدهد و برای سه شرط x=2 داریم :
8D+16E+32F=f(2)=1
12d+32E+80F=f"(2)=1
12D+48E+169F=f""(2)=0
که عدد های D=1/4 و E=-1/16 و F=0 را نتیجه می دهد و در نتیجه جواب :
که در نهایت مسیر کلی بصورت زیر است:
است. البته طراحان جاده ها و سازندگان ریل قطار ها اغلب از چند جمله ای ها برای اتصال استفاده نمی کند و در عوض از خم های
clothoid و Lemniscat استفاده می کنند. چرایی استفاده از خم های بالا نیز به خواص جالب آنها بر می گردد که خود قبل تامل می باشد!
کلمات کلیدی :

نوشته شده توسط رافق مجتهدزاده خیاوی در یکشنبه 87/3/5 و ساعت 12:0 صبح |
نظرات دیگران()