نوشته شده توسط انجمن علمی ریاضیات کاربردی در جمعه 87/11/18 و ساعت 2:58 عصر | نظرات دیگران() نوشته شده توسط انجمن علمی ریاضیات کاربردی در چهارشنبه 87/8/15 و ساعت 2:40 عصر | نظرات دیگران()گراف ها و درخت ها موضوعاتی ساده و در عین حال بسیار کاربردی در ریاضیات هستند. اینگونه که پیشرفت علوم نشان داده , این مباحث هنوز هم جا برای کار دارند و می توان کاربردهای جدیدی را برایشان تعریف کرد. با هم به نمونه های زیر توجه می کنیم.
فیزیکدان آلمانی گوستاو کیرشهف نخستین کسی بود که رفتار ریاضی درخت ها را در ارتباط با تحقیقاتش روی مدارهای الکتریکی تحلیل نمود. اندکی بعد آرتور کیلی از ریاضیات درخت ها برای شمارش همه ایزومرهای مربوط به برخی هیدروکربن ها استفاده کرد. کیلی نشان داد که اگر یک هیدروکربن اشباع شده دارای K اتم کربن باشد آنگاه ?K+? اتم هیدروژن خواهد داشت. مطلب جالب توجه این است که در حدود سی سال پیش نوام چامسکی و همکارانش روش تازه ای را برای بیان ساختار دستوری زبان های طبیعی مانند انگلیسی ابداع کردند. ثابت شده که این تلاش ها در ساختن کامپایلرهای زبان های سطح بالای کامپیوتری بسیار مفید بوده است. در این بررسی از درخت ها اغلب برای مرحله به مرحله ساختن جملاتی با استفاده از یک قاعده معین که از نظر دستوری صحیح هستند استفاده می شود.
نظر شما چیه؟ کاربرد درخت ها جالب نیست؟
نوشته شده توسط انجمن علمی ریاضیات کاربردی در یکشنبه 87/6/17 و ساعت 1:0 عصر | نظرات دیگران()یکی از دوستان اطلاعات بیشتری در مورد جایزه فیلدز خواسته بود.
وقتی داشتم دنبال اون اطلاعات می گشتم به اطلاعات زیر برخوردم. فکر می کنم دونستن مفید باشه.
در مورد کسانی که جایزه رو نگرفتند اونطور که خودم یادمه گریشا پرلمن این جایزه رو نگرفت. فکر می کنم به این دلیل که معتقد بود اون تنها کسی نبوده که وری اون مساله کار کرده بود.
باز هم دنبال اطلاعاتی راجع به فیلدز م یگردم.
جوایز ریاضی در سال 2005
جوایز استیل
انجمن ریاضی امریکا هر ساله سه جایزه به نام جوایز استیل (Leroy P.Steel Prizes) در زمینه های ((مجموعه آثار و خدمات))،((اثر تحقیقی عمیق و درون ساز))،((اثر توصیفی)) اعطا میکند.در سال 2005، ایزرائیل گلفاند به خاطر آثار متنوع و عمیقی که خود همکارانش طی بیش از پنجاه سال در شاخه های مختلف ریاضیات پدید آورده اند جایزه مجموعه آثار و خدمات را به خود اختصاص داد.گلفاند در اوکراین فعلی متولد شد و بیش از پنجاه سال استاد دانشگاه مسکو بود.او آثار مهمی در جبر باناخ،معادلات دیفرانسیل جزئی،جبر های لی بینهایت بعدی،هندسه انتگرال،تبدیل رادون،و کاربرد های گوناگون ریاضیات دارد.جایزه ی اثر تحقیقی عمیق و درون ساز به رابرت لنگ لندز به خاطر مقاله ی معروف سال 1970 او که در آن ((برنامه لنگ لندز)) مطرح شد تعلق گرفته است. این دستاورد نقطه ی عطفی در نظریه ی نوین اعداد محسوب می شود.جایزه ی اثر توصیفی به برانکو گرونباوم اهدا شد.اثر مورد نظر،کتاب چندبرهای محدب(Convex Polytopes) اوست که در 35 سال اخیر مرجع اصلی و سرچشمه ی بسیاری از تحقیقات ذی ربط در رشته های مختلف ریاضی بوده است.
جایزه ی ولف
جایزه ی ولف سال 2005 به مبلغ مجموعا صد دلار مشترکا به گرگوری مارگولیس و سرگی نویکوف اهدا شد.هر دو ریاضیدان از برندگان پیشین مدال فیلدز،روسی تبار،و در حال حاضر مقیم آمریکا هستند.مارگولیس به مناسبت آثارش در جبر و جبر هندسی و نویکوف به خاطر کارهایش در توپولوژی و فیزیک ریاضی شهرت دارند.
ادامه مطلب...
نوشته شده توسط انجمن علمی ریاضیات کاربردی در شنبه 87/2/28 و ساعت 3:50 عصر | نظرات دیگران()
28 اردیبهشت روز ریاضیاته. انجمن علمی ریاضی قصد داره به تلافی دهه ریاضیات که در سکوت برگزار شد تو این روز یه حرکتی کنه. دانشجویان لطفا پیشنهادات خودشون رو متناسب با توان انجمن و.. و دانشگاه، ذکر کنند ( تو قسمت نظرات شما).
نوشته شده توسط انجمن علمی ریاضیات کاربردی در چهارشنبه 87/1/28 و ساعت 5:7 عصر | نظرات دیگران()حساب دیفرانسیل و انتگرال در آغاز برای برآورده کردن نیازهای دانشمندان قرن 17 ابداع شد.البته لازم به ذکر است ریشه های این علمرا میتوان تا هندسه کلاسیک یونانی میتوان ردیابی کرد. حساب دیفرانسیل و انتگرال به دانشمندان امکان می داد شیب خمها را تعریف کنند، زاویه آتشباری توپ را برای حصول بیشترین برد بدست آورند، و زمانهایی که سیارات نزدیکترین و دورترین فاصله را از هم دارند،پیش بینی کنند. پیش از پیشرفتهای ریاضی که به کشف بزرگ آیزاک نیوتن و لایب نیتس انجامید،یوهانس کپلر منجم با بیست سال تفکر،ثبت اطلاعات،و انجام محاسباث سه قانون حرکت سیارات را کشف کرد
اول: هر سیاره در مداری بیضی شکل حرکث میکندکه یک کانونش در خورشید است
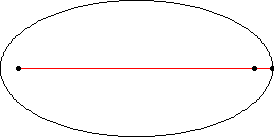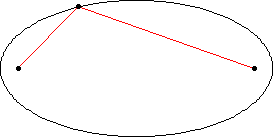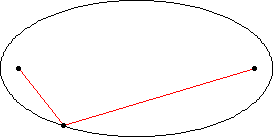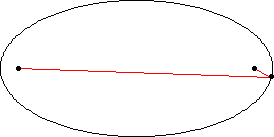
دوم: خط واصل بین خورشید و ستاره در مدتهای مساوی مساحات مساوی را طی میکنند
نوشته شده توسط انجمن علمی ریاضیات کاربردی در یکشنبه 87/1/4 و ساعت 9:0 عصر | نظرات دیگران()سلام با اینکه قبلا هم یه مطلب در مورد منطق فازی تو بلاگ داشتیم( منطق فازی )اما به نظر من این منطق و ظهور اون بقدری مهمه که باید تمام و کمال نسبت به اون اطلاعات داشته باشیم. به نظر من تو این دهه منطق فازی پیشرفتهای شگرفی خواهد داشت و از اون ممهمتر اینکه روی تمام علوم تاثیر خواهد گذاشت.
حالا یه مطلب دیگه از منطق فازیریاضیات فازی یک فرا مجموعه از منطق بولی است که بر مفهوم درستی نسبی، دلالت می کند. منطق کلاسیک هر چیزی را بر اساس یک سیستم دوتائی نشان می دهد ( درست یا غلط، 0 یا 1، سیاه یا سفید) ولی منطق فازی درستی هر چیزی را با یک عدد که مقدار آن بین صفر و یک است نشان می دهد. مثلاً اگر رنگ سیاه را عدد صفر و رنگ سفید را عدد 1 نشان دهیم، آن گاه رنگ خاکستری عددی نزدیک به صفر خواهد بود. در سال 1965، دکتر لطفی‌زاده نظریه سیستم‌های فازی را معرفی کرد. در فضایی که دانشمندان علوم مهندسی به دنبال روشهای ریاضی برای شکست دادن مسایل دشوارتر بودند، نظریه فازی به گونه‌ای دیگر از مدل‌سازی، اقدام کرد
منطق فازی معتقد است که ابهام در ماهیت علم است. بر خلاف دیگران که معتقدند که باید تقریب‌ها را دقیق‌تر کرد تا بهره‌وری افزایش یابد، لطفی‌زاده معتقد است که باید به دنبال ساختن مدل‌هایی بود که ابهام را به عنوان بخشی از سیستم مدل کند. در منطق ارسطویی، یک دسته‌بندی درست و نادرست وجود دارد. تمام گزاره‌ها درست یا نادرست هستند. بنابراین جمله «هوا سرد است»، در مدل ارسطویی اساساً یک گزاره نمی‌باشد، چرا که مقدار سرد بودن برای افراد مختلف متفاوت است و این جمله اساساً همیشه درست یا همیشه نادرست نیست. در منطق فازی، جملاتی هستند که مقداری درست و مقداری نادرست هستند. برای مثال، جمله "هوا سرد است" یک گزاره منطقی فازی میباشد که درستی آن گاهی کم و گاهی زیاد است. گاهی همیشه درست و گاهی همیشه نادرست و گاهی تا حدودی درست است. منطق فازی میتواند پایه‌ریز بنیانی برای فن‌آوری جدیدی باشد که تا کنون هم دست‌آورد‌های فراوانی داشته است کاربرد منطق فازی از منطق فازی برای ساخت کنترل کننده های لوازم خانگی از قبیل ماشین رختشویی (برای تشخیص حداکثر ظرفیت ماشین، مقدار مواد شوینده، تنظیم چرخهای شوینده) و یخچال استفاده می شود. کاربرد اساسی آن تشخیص حوزه متغیرهای پیوسته است. برای مثال یک وسیله اندازه گیری دما برای جلوگیری از قفل شدن یک عایق ممکن است چندین عضو مجزا تابعی داشته باشد تا بتواند حوزه دماهایی را که نیاز به کنترل دارد به طور صحیح تعریف نماید. هر تابع، یک ارزش دمایی مشابه که حوزه آن بین 0 و 1 است را اختیار می کند. از این ارزشهای داده شده برای تعیین چگونگی کنترل یک عایق استفاده می شود From: riazi2000.blogfa.com 
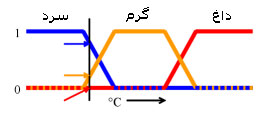در شکل روبرو، سرد بودن، گرم بودن و داغ بودن، توابعی برای مقایسه درجه حرارت هستند و هر نقطه ای روی این خطوط می تواند دارای یکی از سه ارزش بالا باشد. به عنوان مثال برای یک درجه حرارت خاص که در شکل با یک خط نشان داده شده است، می توان گفت: «مقداری سرد است»،«اندکی گرم است» یا «اصلاً داغ نیست». حال با مثال دیگری اهمیت این علم را بیشتر درک مینمائیم: یک انسان در نور کافی قادر به درک میلیونها رنگ میباشد.ولی یک روبوت چگونه میتواند این تعداد رنگ را تشخیص دهد؟ حال اگر بخواهیم روباتی طراحی کنیم که قادر به تشخیص رنگها باشد از منطق فازی کمک میگیریم و با اختصاص اعدادی به هر رنگ آن را برای روبوت طراحی شده تعریف میکنیم
از کاربردهای دیگر منطق فازی میتوان به کاربرد این علم در صنعت اتومبیل سازی(در طراحی سیستم ترمز ضد قفل و کنترل موتور برای بدست آوردن بالاترین راندمان قدرت)،در طراحی بعضی از ریزپردازنده ها و طراحی دوربینهای دیجیتال اشاره کرد
دانشجویانی که اطلاعات جامعتری در مورد منطق فازی دارند اطلاع بدن تا استفاده کنیم. متاسفانه در حال حاضر تو کتابخانه دانشگاه فقط یه کتاب در مورد منطق فازی داریم.
نوشته شده توسط انجمن علمی ریاضیات کاربردی در سه شنبه 86/12/28 و ساعت 1:0 صبح | نظرات دیگران()آنالیز ریاضی
آنالیز شاخه ای از ریاضیات است که با اعداد حقیقی و اعداد مختلط و نیز توابع حقیقی و مختلط سر و کار دارد و به بررسی مفاهیمی از قبیل پیوستگی ،انتگرال گیری و مشق پذیری می پردازد. از نظر تاریخی آنالیز در قرن هفدهم با ابداع حساب دیفرانسیل و انتگرال توسط نیوتن و لایپ نیتس پایه ریزی شد. در قرن هفدهم و هجدهم سر فصل های آنالیزی از قبیل حساب تغییرات،معادلات دیفرانسیل با مشتقات جزئی، آنالیز فوریه در زمینه های کاربردی توسعه فراوانی یافتند و از آنها به طور موفقیت آمیز در زمینه های صنعتی استفاده شد. در قرن هجدهم تعریف مفهوم تابع به یک موضوع بحث بر انگیز در ریاضیات تبدیل شد. در قرن نوزدهم کوشی با معرفی مفهوم سری های کوشی اولین کسی بود که حساب دیفرانسیل و انتگرال را بر یک پایه منطقی استوار کرد.. در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه داد، در اواخر قرن نوزدهم وایراشتراس مفهوم حد را معرفی کرد و نتایج کار خود بر روی سریها را نیز ارائه داد در همین دوران ریاضیدانان با تلاش های زیاد توانستند انتگرال ریمان را اصلاح نمایند . در اوایل قرن بیستم هیلبرت برای حل معادلات انتگرال فضای هیلبرتی را تعریف و معرفی نمود.از آخرین تحولات در زمینه آنالیز می توان به پایه گذاری آنالیز تابعی توسط یک دانشمند لهستانی به نام باناچ نام برد
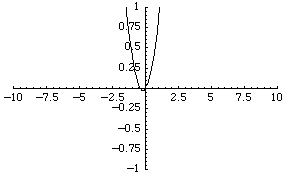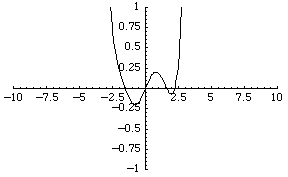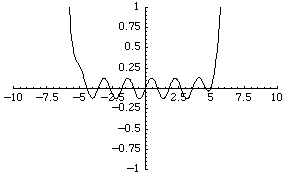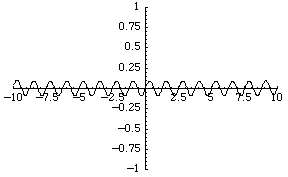
نوشته شده توسط انجمن علمی ریاضیات کاربردی در دوشنبه 86/12/27 و ساعت 6:40 عصر | نظرات دیگران()
نوشته شده توسط رافق مجتهدزاده خیاوی در پنج شنبه 86/12/16 و ساعت 12:0 صبح | نظرات دیگران()
نگاره ای ازچند جمله ای درجه 36
اثر بهمن کلانتری
ادامه مطلب...
نوشته شده توسط انجمن علمی ریاضیات کاربردی در دوشنبه 86/11/29 و ساعت 2:48 عصر | نظرات دیگران()
|
|
|
|
